Methodology for Selection of Material Models for Plastics Impact Simulation

Hubert Lobo, DatapointLabs Ithaca, NY

Abstract

The volume of plastics that are subjected to impact simulation has grown rapidly. In a previous paper, we discussed why different material models are needed to describe the highly varied behavior exhibited by these materials. In this paper, we cover the subject in more detail, exploring in depth, the nuances of commonly used LS-DYNA material models for plastics, covering important exceptions and criteria related to their use.

Keywords: Plastics, Elastomers, MAT 24, MAT 19, MAT 89, Material model, Ductile-brittle transition.

Introduction

High strain-rate properties have many applications in the simulation of automotive crash and product drop testing. With the high volume of plastics used in the products of today, there is an overwhelming need to model the behavior of these complex materials in an accurate manner. Previously, we showed that plastics exhibit different kinds of high strain rate behavior and that it was important to use an appropriate LS-DYNA material model for valid simulation results. In this paper, look in more detail at the modelling of ductile and brittle rate dependency of plastics. Important distinctions in material behavior that dictate the choice of MAT19 over MAT24 are covered. The modelling of rate dependency of the failure stress as permitted by MAT19 is also covered.

A dangerous failure mode of materials is related to ductile-brittle transitions due to rate-dependency. Modelling this kind of behavior needs to be done carefully so that this behavior can be captured. We describe the use of MAT 24 for this purpose and limitations of its use. We look into the pros and cons of MAT89 as a substitute for the MAT24 model and the value conferred by its flexibility. Other candidate models will be considered. Finally, we give more thought to the question of the modelling of rate dependency itself. The validity of the Cowper-Symonds model for use with plastics is questioned and alternate strategies are proposed for the improvement of solution accuracy.

Fundamentals Of Plastics Rate Dependency

Polymers are highly complex materials, whose mechanical properties vary with stress level, time (rate), temperature and many other parameters. The result is non-linear behavior that is not easily captured by conventional material models which have their roots in metals theory. The following kinds of effects must be considered.

Dependency of the stress-strain relation on stress level is unique for plastics. Hyper-elastic materials exhibit highly non-linear elastic behavior but show no plasticity. Metals on the other hand, show highly linear elastic behavior, with plasticity becoming relevant only post-yield. Plastics stress-strain behavior is neither hyper-elastic nor linear. Contrary to metals, the onset of plastic strain occurs prior to yield. Additionally, the elastic behavior is non-linear. Attempts to approximate this behavior using metals theory comprise a poor approximation of the actual behavior leading to the following compromises. Attempting to predict behavior with fidelity to the onset of true plastic behavior causes an under-prediction of the stiffness of the material at low stresses. Attempting to be true to the elastic modulus of the material results in an overprediction of the plastic strain as one is forced to assume the onset of plastic strain much before it occurs in real life. The consequences and modelling of this behavior are discussed in more detail in the paper by Lobo and Hurtado [5].

In describing the rate-dependent behavior of a polymer, additional complications arise. Up to the vicinity of yield, we note that certain plastics exhibit significant rate-dependency of modulus while others do not [3]. This is in distinct contrast to metal behavior where the expected behavioral trend is toward no dependency of modulus with strain rate, as exemplified by the MAT24 type material model. A consequence of this finding is that polymers exhibiting rate dependency of modulus cannot be described by a MAT24 type model. The use of MAT24 for such materials will result in significant error in stiffness predictions. These and other limitations of MAT24 must be considered carefully in selection of a material model for describing rate dependency of plastics. The combination of the effect of stress as well as strain-rate on the rate dependent stress-strain relationship of plastics, as explained above creates a complex situation, that is only crudely approximated with currently available material models. Nonetheless, by proper selection, is possible to conduct meaningful simulation by selecting existing material models that most closely match the behavior shown by the material data.

With respect to the rate-dependency of the plasticity behavior, a remarkable consistency is observed for a large variety of plastics. A predominant trend exists toward agreement with the Eyring equation, which is characterized as a linearly increasing relationship between yield stress vs. log strain rate. The obvious exception is the case of plastics exhibiting brittle failure where the result is more noisy. In contrast, the Cowper-Symonds model which is used extensively for metals and is implemented in MAT24 fails to capture the right trend leading to modelling inaccuracy in modelling rate dependency of plastics.

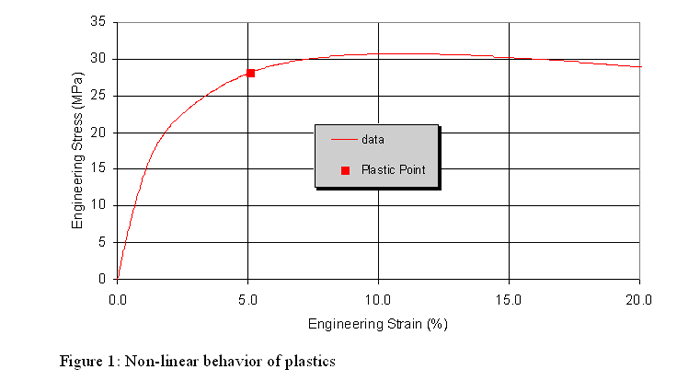
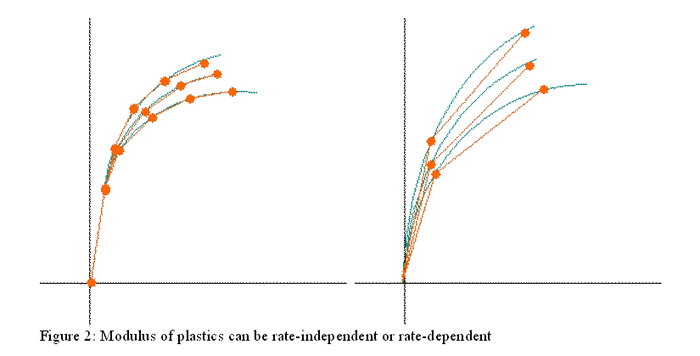
The addition of fiber reinforcements to plastics is a common practice to increase the strength of these materials. In addition to an increase in stiffness, the nature of the failure changes when fillers are added. In the extreme cases, such as highly glass filled plastics, the failure changes from ductile to brittle. Interestingly, with intermediate fiber loadings, there is a gradual change from ductile to brittle failure with the increase in strain rate. This variation in post-yield behavior with strain rate is not easily captured in available material models today.

Implementation In LS-DYNA 24

The LS-DYNA MAT24 is the most widespread material model in use today for the modelling of crash, drop and other rate-dependent phenomena. It's simplest and most commonly used nuance couples a Cowper-Symonds model with an elastic-plastic curve as follows. The elastic region is modelled as rate independent up to an arbitrarily or otherwise determined yield point, beyond which the stress-strain curve at the lowest strain rate of interest is decomposed into an elastic-plastic model. This produces a curve of stress v. plastic strain (ES v. EPS), hereafter referred to as the plasticity curve. As seen in Figure 2a, the definition of yield as seen in metals does not correspond to that used in this context for plastics. The accuracy of this model, when applied to plastics, depends on the stress-strain relationship being linear up to the chosen yield point, that this initial linearity is not rate dependent and that the shape of the plasticity curve is uniform and independent of strain rate. This is simply not true for most plastics. Since plastics are non-linear elastic followed by elastic-plastic, an arbitrary choice is usually made somewhere along the increasing part of the stress-strain curve denoting the onset of plastic strain. In recent work, we show a method for accurately measuring this "plastic point" [5]. Using the plastic point, however is not always feasible because of the limitation of linear elasticity.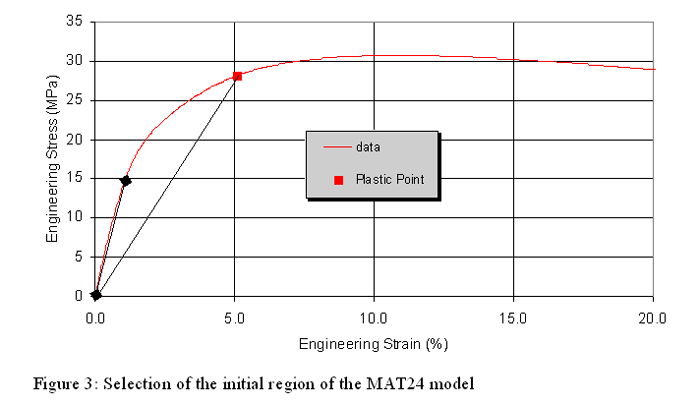

As can be seen in Figure 3, fidelity to the linear elastic region results in an overprediction of plastic strain because the material continues to be elastic at stresses far exceeding the "linear-elastic" region. On the other hand, using a secant modulus to describe the behavior up to the plastic point results in a material model that significantly under-predicts the stiffness of the material in the elastic region. Currently, with the the MAT24 model, there is no recourse other than to choose, pragmatically, a plastic point that is somewhere in between these extremes, often leaning toward the first strategy so as to be as close as possible to the stress-strain data. Once EMOD has been chosen, it is a simple matter to discretize the static stress-strain and convert the data into plastic strains following the normal rules of the elastic plastic model. Applying the Cowper-Symonds equation, it is now possible to scale this curve to other strain rates. The equation has the advantage of smooth extrapolation without limits. However, since the equation is incapable of truly describing the rate dependency of the yield phenomenon, it cannot accurately scale the plasticity curve to high strain rates. A possible solution is to use the LCSR option, which permits the submission of a table of scale factors for each strain rate. LCSR is an interesting option which allows fidelity to the test data. However, it must be used with caution. High strain rate data is experimentally difficult to obtain so that there is often scatter in the data. This scatter must be smoothed in some way so that the resultant model contains no spurious behavior. Since we know that the Eyring Equation appears to accurately describe the rate dependency of most plastics, the LCSR table can be derived from a best fit of the yield stress v. log strain rate data. This approach carries two advantages: first, the elimination of noise and second, the ability to extrapolate the model to 'higher that tested' strain rates, since LCSR based MAT24 terminates rate dependency computation when the highest strain rate in the table is exceeded. Using MAT24 with LCSR as described above, we can successfully overcome the limitation of the Cowper-Symonds model in the simulation of plastics rate-dependency.

A serious drawback of MAT24 arises from the fact that the failure strains themselves typically reduce with increasing strain rate. This variation is not accommodated by the model, which assumes that failure strain is constant and independent of strain rate. Failure in MAT_24 occurs when the accumulated plastic strain in an element reaches the value specified in FAIL. At each time step, after the trial stress is computed, if the trial stress is found to be outside the yield surface (VonMises), LS-DYNA scales the stress back to the yield surface and then obtains the accumulated plastic strain by using the material model to calculate the corresponding effective plastic strain (EPS) at the strain rate seen by the element. If this accumulated plastic strain equals FAIL, the element is removed. FAIL is usually chosen by the analyst as largest failure strain in the material data. This is the conservative approach. If the data shows a variation in failure strains with strain rates, a check must be made by the analyst to review the strain-rate experienced by the part, to pick a value of FAIL at that corresponding strain rate. It is clear that with plastics with ductile-brittle transitions or where the failure strain is highly rate dependent that this limitation can have a significant impact on the simulation.

The LCSS option of MAT24 is very useful when the shape of the plasticity curve changes with strain rate. This phenomenon is often observed in plastics. In this case, by submitting a plasticity curve for each strain-rate, we are able to independently describe the stress-strain behavior as a function of strain rate allowing us the ultimate in flexibility offered by the model. It may still be a useful exercise to smooth the rate-dependency using the approach outlined earlier. LCSS however does not offer relief in the modelling of ductile-brittle transitions, because of the limitation of FAIL. Proper implementation of LCSS requires that we extrapolate all the plasticity curves to the largest failure strain (FAIL) that we intend to use in the model. Consequently information regarding the change in failure strain with strain rate is lost.

Polymers such as polycarbonate, polyethylene and polypropylene exhibit long tails of post-yield strain and are capable of absorbing significant energy in this phase of their deformation. Stress-strain curves for plastics that are not brittle in nature go through an inflection or local maximum commonly referred to as the yield point, not to be confused with the von Mises yield which corresponds to the onset of plastic deformation. When handling post-yield behavior, a number of complications arise. Most post yield behavior is accompanied by necking, localized non-uniform deformation, which leads to a condition where the area of cross-section of the deformation zone is unknown. Consequently, the stress is also an unknown and can only be crudely estimated by making some assumptions about the cross-sectional area. The most common one is to assume that the true stress calculation applies in this region as well. A consequence of this assumption is that the slope of the stress-strain curve is seen to gradually increase with increasing strain. In the case of olefinic materials such as polypropylene and polyethylene whose necking phenomenon is more closely equated with unravelling or unzipping of the dendritic structure, it is more likely that the stress remains constant during necking. In any case, to model these regions using MAT24, it is only essential to eliminate negative slopes in the model.

Comparing Other Models To LS-DYNA 24

A number of fiber-filled plastics show considerable rate dependency of modulus followed by very small strains to failure. There is no yield and failure points are coincident. A small amount of plastic strain is accumulated prior to failure. This kind of behavior is extremely difficult to model with accuracy using MAT24 for the following reasons. The stress-strain curves begin to diverge almost immediately as seen in Figure 2b. Consequently, MAT24 will either under-predict the stiffness at low strain rates or vice versa depending on the choice of the modulus E. While this may have quite a bit of impact on the simulation of most plastics, in the case of filled plastics, the effect is even more dramatic because the failure strains are so small, typically 2%. MAT 19, even though it suffers from the deficiency of being a bi-linear model, is better suited and achieves higher fidelity to the experimental data. An added advantage of the model is its ability to precisely indicate the failure envelope of the material via the use of the failure strain v. strain rate dependency option. This effect is often quite marked in such materials and must be modelled with accuracy for good simulation results. Additionally, the model allows failure based on tensile plastic strain only.

MAT89 is an elastic-plastic material model that does not require the user to break up data into elastic and elastic-plastic regions. It is recommended by LS-DYNA to handle the highly complex behavior of ductile-brittle transitions where failure strains can vary anywhere between 100% and 10% for some plastics. With MAT89, the initial stress-strain curve is entered as true stress-strain data. LS-DYNA internally checks the slope of the curve. When this slope falls below the modulus E specified in the material card, the material is assumed to have yielded. The treatment of plasticity then follows MAT24, as described earlier. The LCSR scaling of the stress-strain curve allows this model to be scaled to high strain rates in a manner similar to MAT24. The LCSR table of yield stress v. strain rate is a better choice for modelling rate-dependency that the Cowper-Symonds equation for the same reasons described earlier. The key benefit of MAT89 is the LCFAIL table which enables the entry of failure strains v. strain rate. This feature overcomes the limitation of MAT24, which restricts its ability to model plastics whose failure strains change significantly with strain rate.

Summary And Conclusions

A number of material models exist that could be used for the modelling of polymeric behavior. Constraints in these models limit their ability to capture all the possible behavior types of plastics. It is important, therefore, to select the appropriate material in order to exploit its capabilities to the maximum. In this paper, we have outlined which available models are best suited to handle some of the major classes of plastics. There still remain important behaviors that are not adequately captured by any model. A key deficiency arises when the shape of the stress-strain curve and the failure strains change with strain rates. A suitable solution would be the addition of some kind of LCFAIL option to MAT24.

Acknowledgements

I would like to acknowledge, with thanks, the contributions of Mr. Brian Croop of DatapointLabs and Dr. Suri Bala of LSTC for comments, advice and clarifications on how the models are implemented in LS-DYNA.

References

1. Lobo, H., Lorenzo, J., “High Speed Stress-Strain Material Properties As Inputs For The Simulation Of Impact Situations,” IBEC, Stuttgart, Germany (1997).

2.Grimson, A., Sinopoli, M., Lobo, H., Fedewa, B., “Evaluation of High Strain Rate Test Methods of Thermoplastic Polyolefins Used for Automotive Interior Structural Analyses,” SPE TPO Conference, Detroit, (2003).

3. Croop, B., “Developing Material Model Parameters for Impact Simulation of Plastics and Foams,” ABAQUS User’s Conference, Boston (2004).

4. Perkins, L. and Lobo, H. "A Novel Technique to Measure Tensile Properties of Plastics at High Strain Rates", SPE ANTEC Proceedings, Boston (2005).

5. Lobo, H., Hurtado, J. " Characterization and Modeling of Non-linear Behavior of Plastics", ABAQUS User Conference, Boston (2006).

6. Lobo, H. " Advances in the Measurement and Modeling of Plastics for Impact Simulations", 9th Intenrational LS-Dyna User's Conference, Detroit (2006).