Summer '01 Volume 7.2
 
Articles
 

Rubber and elastomer modeling strategies

Quantification of rubber behavior depends on a large number of factors such as the mode and magnitude of deformation, rate effects, temperature and the environment, and last but not least, the well known Mullins effect. Further, real life scenarios may have the product responding simultaneously to a multiplicity of these conditions. A classic example may be the rubber boot of an automotive CV joint that is simultaneously seeing large deformation, temperature, cyclic loading and oil or grease. To completely describe the material behavior would require a hyperelastic model on an oil-soaked boot rubber over a range of temperatures, with some consideration given to rate dependency. It becomes highly impractical to attempt to model all these situations. Accordingly, one often adopts a strategy that seeks to use the simplest acceptable model that achieves a reasonable approximation of the actual scenario. This strategy may be weighted to include more detailed modeling of the greatest potential sources of failure.

Considerable discussion has been given to the hyperelastic model and the relative merits of different modes of deformation. Different kinds of tests offer different benefits. Other factors not often considered but equally important are cyclic loading effects and the magnitude of deformation. The Mullins effect describes the change in stressstrain behavior that occurs between an initial deformation of a rubber as compared to subsequent loadings. The effect is attributed to microscopic breakage of links in the rubber that weaken it during its initial deformation so that it is weaker in subsequent loadings. For the purposes of simulation, it is particularly important to question whether the Mullins effect is relevant for the situation under consideration because it can have a considerable impact on the material testing as well as on the material model that is used to represent the data. Accordingly, components that are subject to repeated load-unload cycles to the same strain should utilize material data that have been developed on samples after they have been subject to precycling. Here, test specimens are subjected to repeated load-unload cycles to the strain of interest until there is no change in the shape of the curves. The resulting ultimate stress-strain behavior is then used for the model development. It is important to note that such models are not suitable to describe first time deformations. Analogously, products that are subject to varying deformations are not properly described by one individual curve. Conventional hyperelastic models cannot describe such complex behaviors as seen in Figure 2. In such cases, a simpler piecewise approach may prove adequate. Again, being aware of the needs of the simulation will permit the analyst to request the appropriate information at little or no additional cost. Failure to anticipate this need results in expensive retesting. In the worst case, the wrong data is used, resulting in erroneous simulations.
 

Finally, getting this behavior into the analysis usually requires a material model. The hyperelastic material models present a number of options to aid in a best fit of the material data. The Mooney-Rivlin model is by far, the most common model in use today. It presents many advantages in terms of being able to handle the different kinds of behavior seen in rubbers. The ability to increase the number of modes permits the handling of large strain behaviors with some level of dexterity. The objective of any model development effort, however, is to fit the data at as low a number of modes as possible. As stated above, an important guideline in model fitting is advance knowledge of the strain range of interest. The Ogden model also offers great versatility in fitting the complex behavior of rubber. The choice between these models is often governed by the goodness of fit to the actual data. However, as pointed out by Boyce [1],


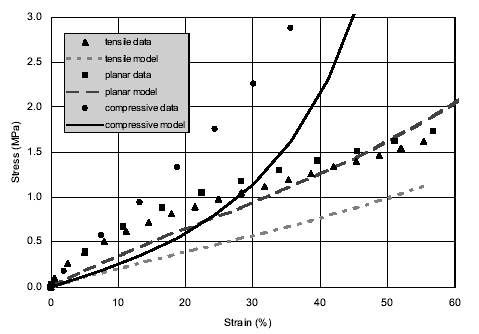
Figure 2. Arruda-Boyce model is unable to fit non precycled rubber

these empirical models may not be as robust as those based on statistical mechanics. The more recent Arruda-Boyce model is a promising model that has a statistical mechanics basis. This model presupposes a certain kind of rubber behavior so that it has the capability to work well for materials that obey its laws. A big advantage of this approach is that the model can then predict behavior in multiple modes from data taken in only one mode: tension. We find in our work, however, that there are some materials that do not obey its laws so that the need for more detailed characterizations cannot be eliminated. Additionally, the Arruda-Boyce model does not handle the initial deflection region well, rendering it not as useful for small deformation modeling of rubbers. In comparison, the Mooney- Rivlin model does a better job because it has the potential of a greater number of coefficients and is able to handle such behavior. Further, we observed that the Arruda-Boyce model has difficulty with biaxial (compressive) data [2].

Careful consideration to the needs of a particular simulation can yield considerable benefits when modeling rubber materials.

References

[1] M.C. Boyce and E.M. Arruda, J. Rubber Chem. Tech v.73, pp 504-523 (2000)
[2] D.J. Siebert and N. Schoche, J. Rubber Chem. Tech, v.73 pp 366-384 (2000)

DatapointLabs unveils new e-commerce enabled web-site



Figure 1. New home page of DatapointLabs.com

ITHACA, NY: May 7, 2001-DatapointLabs launches its new e-commerce site www.datapointlabs.com to lead the industry as the first web-enabled materials testing company. The new web site offers all the information a user needs to make an easy online purchase, and serves as a resource for over 150 tests used for research and development, product design, automotive certification and quality control. It allows users control of their orders and past orders history. "We are trying to provide a virtual expert on-line, ready to guide our users to select the tests that best meet their material testing needs. Of course, our laboratory staff is always here to assist the user,"
states Hubert Lobo, President.

TestPaks® Alliance Program

The new site also gives greater exposure to DatapointLabs? TestPaks® Alliance Partners. Here, users can view details about CAE programs supported by DatapointLabs. TestPaks® for each program are conveniently categorized permitting CAE analysts to select the material models they need. Guidance is provided on the use of the material models that are supported.

Dale Hummel named CRM Manager; new personnel added

Dale Hummel has been appointed Customer Relations Manager. Customer relations becomes crucial in the new Internet economy when people rely on the impersonal world- wide-web to communicate and transfer information. "We are fortunate to have such an experienced manager to take up this role at DatapointLabs, In conjunction with his current role of Operations Manager, Dale is the eyes and ears of the customer in the laboratory" says Hubert Lobo, company president. Kelly Evans, a recent graduate from Ithaca College has joined DatapointLabs as an Administrative/ Sales Associate. Kelly is a published writer and an avid softball player.

New Tests

Low Temperature Bend Test- ASTM D2136

Fabrics coated with rubber or rubber-like materials display increased stiffening when exposed to low temperatures. This test describes a pass/fail procedure by which material flexibility at a specified low temperatures can be determined.

HDT(ASTM D648) & VIcat (ASTM D1525)

This classic bend test measures the temperature where a specified flexural load cannot be sustained by the material. The Vicat test is similar but uses a point stress instead.

Expanded ISO Test List

The following ISO tests have been added to the on-line catalog.

ISO 527-1 Tensile tests
ISO 604 Compressive tests
ISO 178 Flexural tests
ISO 180 Izod impact tests
ISO 179 Charpy impact tests
ISO 6603-2 Instrumented impact tests
ISO 899 Creep tests
ISO 75-1 Heat deflection temperature
ISO 11357 DSC
ISO 1183 Density

Upcoming events

ABAQUS User's Conference. May 30-June 1, Maastricht, The Netherlands.
FIDAP and Polyflow User's Group Meeting. June 19, Skokie, IL.
ISO TC61 Meeting. September 9-15, Berlin, Germany.
Moldflow 2001 Internaltional User Group Meeting. September 17-19, Boston, MA.

Articles discuss use of engineering properties in simulation

Plastics researchers, CAE analysts, processors and producers gathered at the Dallas Convention Center May 7-11 to attend the ANTEC 2001 conference and exhibition which showcased the latest developments in the plastics industry. Of almost 1000 papers presented, we list below our pick of noteworthy papers.

We noted a dramatic increase in the use of full 3D for injection molding and extrusion CAE. Advances were seen for rotational molding simulation. Significant progress was reported in the understanding of crystallization phenomena. Novel work on finite element analysis for impact and puncture simulation was also presented.

Injection molding

Modeling the Melting Process of Polymer Pellets Caused by Friction (91), Yung, K.L., Xu, Yan, and Lau, Francis.

The Effect of Inertia on Fill Pattern in Injection Molding (739), Costa, Franco S., Ray, Shishir, Friedl, Chris, Cook, Peter S., and Xu, Shoudong.

Prediction of the Impact Behavior of Injection Molded Plates (82),Viana, J.C., Cunha, A.M. and Billon, N.

Numerical Simulation of Injection Molding of Semicrystalline Thermoplastics (633), Guo, Jianxin and Narh, Kwabena A.

A Novel Three-Dimensional Analysis of Polymer Injection Molding (740), Chang, Rong-Yeu and Yang, Wen-Hsien.

Structure Performance of Thin-Wall Injection Molded Parts (77), Chen, S.C., Jong, W.R., Chang, Y.P., Kang, Y., Peng, H.S., Huang, L.T., Yang, L.K., Chang, C. T., and Luo, R.C.

3D Solid Brick Element Injection Molding Simulation-A Time Effective Solution (44), Berhardt, Anne, Bertacchi, Giorgio, and Moroni, Antonino.

Analysis of Internal Structure of Injection-Molded Parts Based on a Three-Dimensional Simulation Software (343),
Hoffmann, S. and Michaeli, W.

New Solidification Models for the Simulation of the Injection Molding Process (592), Moneke, Martin, Amberg, Joachim, Bastian, Martin and Alig, Ingo.

Full 3-D Prediction of Warpage of Injection Molded Parts (279), Inoue, Y., Imai, K., Takahara, M., Murayama, Y., Matsuoka, T., Shinoda, K., and Mori, Y.

Three-Dimensional Simulation of Injection-Compression Molding of a Compact Disk (736), Chang, Rong-Yeu, Chang, Wen-Ya, Yang, Wen-Hsien, Yang, Wen-Li, and Hsu, David C.

Three-Dimensional Modeling of Gas-Assisted Injection Molding (733), Chang, Rong-Yeu and Yang, Wen-Hsien

Experimental and Numerical Analysis of Thin-Wall Injection Molding with Micro-Features (718), Yu, Liyong, Koh, Chee Guan, Koelling, Kurt W., Lee, L., James, and Madou, Marc J.

Rotational Molding

Non-Isothermal Melt Densification in Rotational Molding (787), Tiang, J.S. and Bellehumeur, C.T.

Extrusion

Flow Analysis in Single Screw Extruders (177), Lawal, Adeniyi and Railkar, Sudhir.

Three-Dimensional Numerical Analysis of the Single Screw Plasticating Extrusion Process (735), Chang, Rong-Yeu, Hsu, Che- Wei, Yang, Wen-Hsien, Yang, Wen-Li, and Hsu, David C.

Blow Molding

Thermomechanical Modeling, Microstructure Development and Part Performance in Stretch Blow Molding (117), Laroche, D., DiRaddo, R., and Brace, J.

Large Part Blow Molding (LPBM) of HDPE Resins: Parison Extrusion Behavior and Its Relationship with the Resins: Rheological Parameters (371), Jivraj, N., Sehanobish, K., Ramanathan, R., Garcia-Rejon, A., and Carmel, M.

Thermoforming

Modeling of the Effect of Slip in Plug-Assisted Thermoforming (94), Laroche, D., Collins, P., and Martin, P.

Robust Simulation for the Heating Stage in Thermoforming (114), Yousefi, A., Bendada, A., and DiRaddo, R.

Experimental Investigation of Slip in Plug-Assisted Thermoforming (630), Collins, P., Martin, P., Harkin-Jones, E., and Laroche, Denis.

Viscoelastic Material Characterization at Large Deformation (392),Kouba, Karel, Novotny, Petr, and Kech, Armin.

FEA/Impact Simulation

Simulation of the Puncture Resistance of a Thermoformed Syringe Pack (879), Christopherson, Roy and Briere, Marc.

Kinematics of Quasistatic Inflation of a Catheter Balloon Made of Elastomeric Material: Simulation and Experiment (124), Guo, Xiaoping and Bednarek, Michael.

Measurement of Strain Rate-Dependent Material Properties for Polymers (713), Keuerleber, M., Eyerer, P., and Buhring, J.

Experimental and Analytical Verification of Plastics Material Models for Automotive Crashworthiness Applications (597), Pitrof, Stephen M. and Lee, Michael C.

Plastic Material Modeling for Vehicle Crash Simulation Using LS-DYNA (897), Xiao, Xinran Sharon.

Failure Analysis of High Density Polyethylene in Engineering Applications (352), Zhou, Wen and Chudnovsky, Alexander.

Material Characterization

The Role of Melt Dynamics in Shear-Enhanced Crystallization of Isotactic Polypropylene (841), Oberhauser, James
P., Thurman, Derek W., and Kornfield, Julie.

Application of the Time Temperature Shift Principle to the Material Behavior of Rubber under High Deformations (330), Grambow, Andreas and Haberstroh, Edmund.

Measuring the Nonlinear Viscoelastic Material Properties of Thermoplastic Materials by DMA (492), Schroder, O. and Schmachtenberg, E.

Friction Properties of Thermoplastics in Injection Moulding (25), Ferreira, E.C., Neves, N.M., Muschalle, R., Pouzada, A.S.

Bulk Moduli from Enthalpy and Volume Data Obtained During Physical Aging Experiments (684), Slobodian, P., Pelisek, B., Kubat, J., and Saha, P.

An Advanced (HMG) Short Glass-Fiber Reinforced Nylon 6: Part II Mechanical Performance (1055), Kagan, Val A., McPherson, Rowena, and Chung, Jerry S.

Reinforced Plastic Design: Tensile Versus Flexural Fatigue (455), Krohn, John A., Novak, Glen E., and Wyzgoski, Michael G.

A Model and Parameter Formulation of Stress-Induced Crystallization Kinetics of Polymers (634),Guo, Jianxin and Narh, Kwabena A.

Modeling Structural Recovery: Analysis of the Peak Shift Method(1039),Zheng, Yong, Simon, Sindee L., and McKenna, Gregory B.

Extensional Flow Properties from Entrance Pressure Measurements Using Zero Length Die Versus Bagley Correction (196),Sunder, J. and Goettfert, A.

Flow Instabilities of Several Linear Polyethylenes in Capillary Experiments and Effect of Die Materials (521), Larrazabal, Hector J. and Hrymak, Andrew N.

Three-Dimensional Non-Isothermal Numerical Analysis of Multi-Layer Coextrusion (732), Chang, Rong-Yeu, Ke,
Chao-Sheng, Yang, Wen-Hsien, Yang, Wen- Li, and Hsu, David C.

Melt Flow Simulation and Measurement of Extensional Viscosity in Planar Hyperbolic Dies (243), Olley, P.,Martyn, M.T., Spares, R., Groves, D., and Coates, P.D.